lacar1601
Well-Known Member
I propose two conceptually related brain-busting questions in geometry. I myself don't know the answers to these questions, but it would be interesting to see if someone here can provide some hard proof for the answers. If nothing else, I encourage everyone to post a silly but creative (and relevant) response even if the answer is wrong.
WARNING: Thinking ahead.
1) BACKGROUND- In analytical geometry, we know that a line can be composed of a set of all points that satisfy some linear relationship. Since a line extends into infinity, we can say that there are an infinite number of points that can make up that line.
Now take the concept of a line segment, which is a line bounded between two distinct, finite points. Even a line segment consists of an infinite number of points because points, as dimensionless entities, must fill every nook and cranny of that line into the infinitesimal.
SETUP: Suppose we have 2 line segments, AB and CD, with CD having longer length than AB.
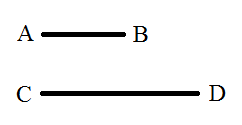
QUESTION: Which line has more points?
2) BACKGROUND- Suppose we have a rectangle of some known area (say, 64) that is bounded by the x-axis and 2 vertical segments that are equidistant from the y-axis as shown.
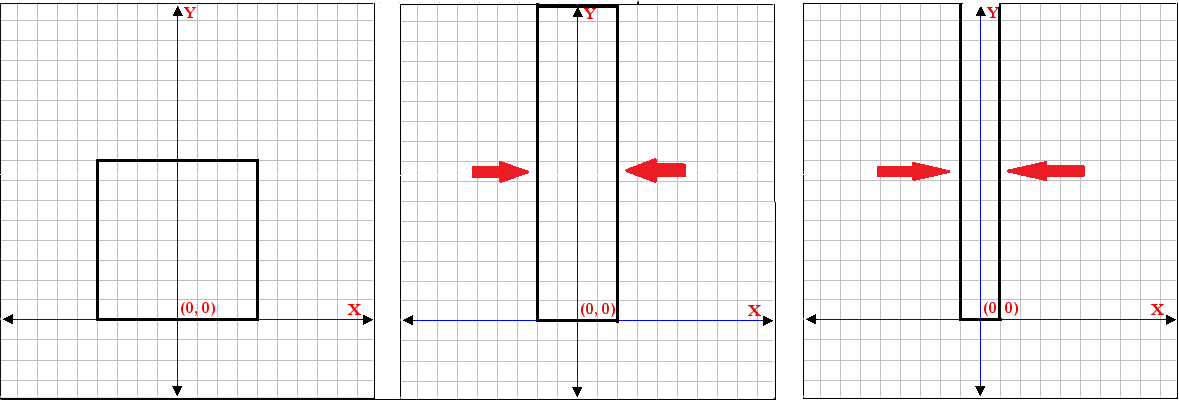
Imagine that we can change the size of the rectangle by moving the two vertical edges along the x-axis, except that we also impose the constraint that the area of the rectangle must remain the same as it was originally. Then as we move the two vertical edges closer together, the height (y-direction dimension) of the rectangle increases to maintain the area.
SETUP: Suppose we have two such cases, with one rectangle having an area of 4 and another having an area of 5. Imagine that we keep squeezing both rectangles as described above so that their heights keep getting larger and larger until the two vertical lines join.
QUESTION: Which rectangle would have the greater height?
WARNING: Thinking ahead.
1) BACKGROUND- In analytical geometry, we know that a line can be composed of a set of all points that satisfy some linear relationship. Since a line extends into infinity, we can say that there are an infinite number of points that can make up that line.
Now take the concept of a line segment, which is a line bounded between two distinct, finite points. Even a line segment consists of an infinite number of points because points, as dimensionless entities, must fill every nook and cranny of that line into the infinitesimal.
SETUP: Suppose we have 2 line segments, AB and CD, with CD having longer length than AB.
QUESTION: Which line has more points?
2) BACKGROUND- Suppose we have a rectangle of some known area (say, 64) that is bounded by the x-axis and 2 vertical segments that are equidistant from the y-axis as shown.
Imagine that we can change the size of the rectangle by moving the two vertical edges along the x-axis, except that we also impose the constraint that the area of the rectangle must remain the same as it was originally. Then as we move the two vertical edges closer together, the height (y-direction dimension) of the rectangle increases to maintain the area.
SETUP: Suppose we have two such cases, with one rectangle having an area of 4 and another having an area of 5. Imagine that we keep squeezing both rectangles as described above so that their heights keep getting larger and larger until the two vertical lines join.
QUESTION: Which rectangle would have the greater height?

